CGAL AlphaShape算法应用

​ 使用该算法的初衷是想找到一个二维点集的有序边界，调用到CGAL中的Alpha_shape2。但是CGAL中的Alpha_shape2获取到的segment是随机的，也就是各个端点是无序的，如下图：

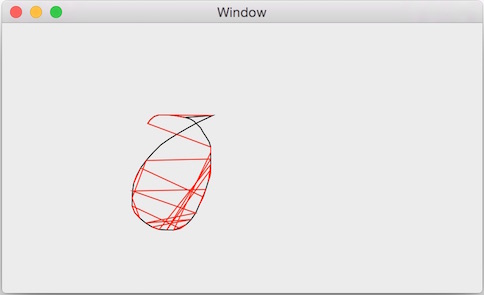
而我们需要的是有序边界，如下图所示：

/*
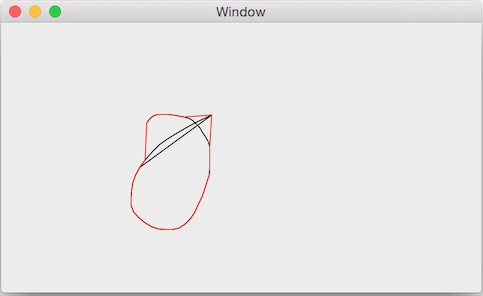
1. 计算Alpha_Shape2
2. 获取segment端点坐标存入points_in_segment
3. 计算points_in_segment vector内所有点的重心barycenter
4. 构造aBary vector，aBary[i] = atan2(points_in_segment[i].y - barycenter.y, points_in_segment[i].x - barycenter.x);
5. 对aBary排序
*/

// alpha shape
typedef K::FT                                                FT;
typedef K::Point_2                                           Point2f;
typedef K::Segment_2                                         Segment2f;
typedef CGAL::Alpha_shape_2<Triangulation_2>                 Alpha_shape_2;

std::list<Point2f> points;
//构造输入点集,下略
...
Alpha_shape_2 A(points.begin(), points.end(),
                FTA(10000),
                Alpha_shape_2::GENERAL);
std::vector<Segment2f> segments;
alpha_edges(A, std::back_inserter(segments));
std::cout << "Alpha Shape computed" << std::endl;
std::cout << segments.size() << " alpha shape edges" << std::endl;
std::cout << "Optimal alpha: " << *A.find_optimal_alpha(1) << std::endl;

//获取segment端点坐标
std::vector<Point2f> points_in_segment;
float sumX,sumY = 0.f;
for (auto& seg : segments) {
    Point2f p1 (seg.vertex(0).x(),seg.vertex(0).y());
    points_in_segment.push_back(p1);
    sumX = seg.vertex(0).x() + sumX;
    sumY = seg.vertex(0).y() + sumY;
}
///////////////////alpha_shape2的线段结果是无序的  因此后面需要排序
//获取重心坐标
Point2f barycenter(sumX/points_in_segment.size(), sumY/points_in_segment.size());

std::vector<float> aBary;
std::vector<int> aBaryIndex;
aBary.clear();
aBaryIndex.clear();
for (int j = 0; j < points_in_segment.size(); ++j) {
    aBary.push_back(atan2(points_in_segment[j].y() - barycenter.y(), points_in_segment[j].x() - barycenter.x()));//计算每一段segment端点与重心之间的正切值
    aBaryIndex.push_back(j);
}

//对正切值按照降序排序，返回索引vector
aBaryIndex = Utility::sort_indexes_decline(aBary);

//获取有序边界
std::vector<Point2f> polygon;
for (int j = 0; j < aBaryIndex.size(); ++j) {
    polygon.push_back(points_in_segment[aBaryIndex[j]]);
}

/**
* @Description: 按照vector内数值大小进行索引降序排序
* @Param:
* @return: 排序后的索引数组
* @Author: Mr.Zhou
* @Date: 2020/9/25
*/
std::vector<int> sort_indexes_decline(const std::vector<float> &v)
{
    // 初始化索引向量
    std::vector<int> idx(v.size());
    //使用iota对向量赋0~？的连续值
    std::iota(idx.begin(), idx.end(), 0);
    // 通过比较v的值对索引idx进行排序
    sort(idx.begin(), idx.end(),
         [&v](int i1, int i2) {return v[i1] > v[i2]; });
    return idx;
}