点云采样算法

开发总结 评论

点云的采样算法，分为上采样和下采样。
上采样：进行点云曲面重建时，所获得的点云数量稀缺，则要对点云进行上采样操作，来增加点云数量，以便更好的计算曲面特征。
下采样：大规模点云处理中，由于点的无序性，如果需要对点云进行特征提取或者后处理，通常需要将对全部点云的操作转换到下采样所得到的关键点上，从而达到降低计算量的目的。

下采样

体素下采样

一般最常用的下采样方法为体素化网格的采样方法，即减少点的数量，并同时保持点云的形状特征基本不变，同时基本上保留了空间结构信息。在点云配准、曲面重建、形状识别等算法速度中非常实用。

体素下采样的原理如图 1 所示，首先将点云空间进行网格化，也称体素化，即图 1(b)，网格化后的每一个格子称为体素，在这些划分为一个个极小的格子中包含一些点，然后对这些点取平均或加权平均得到一个点，以此来替代原来网格中所有的点，即图 1(c) 中蓝色的点。显然，网格选取越大则采样之后的点云越少，处理速度变快，但会对原先点云过度模糊，网格选取越小，则作用相反。

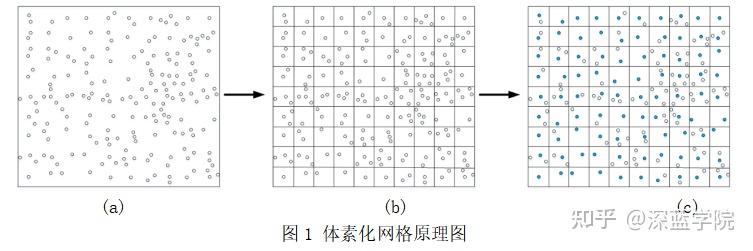
体素下采样的特点是效率高，采样点分布相对比较均匀，同时可以通过控制网格尺寸控制点间距，但是不能精确控制采样点个数。

其核心代码如下：

1
2
3
4
pcl::VoxelGrid<pcl::PointXYZ> sor;    //创建体素网格采样处理对象
sor.setInputCloud(cloud);             //设置输入点云
sor.setLeafSize(0.01f, 0.01f, 0.01f); //设置体素大小，单位：m
sor.filter(*cloud_filtered);          //进行下采样

近似体素重心下采样-ApproximateVoxelGrid

Point Cloud Library (PCL): pcl::ApproximateVoxelGrid< PointT > Class Template Reference

ApproximateVoxelGrid近似体素滤波企图以更快的速度 实现与VoxelGrid 体素滤波相同的下采样，它通过 散列函数（通俗地理解哈希函数 - 知乎）快速逼近质心，而不是精细确定质心并对点云进行下采样。采样结果是近似逼近的体素质心，并不是体素中心。

同一规格体素下，近似体素下采样 比 体素下采样 获取的下采样点数多，且耗时短。

其核心代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <pcl/io/pcd_io.h>
#include <pcl/filters/approximate_voxel_grid.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/console/time.h>

using namespace std;

int main()
{
	//--------------------------------- 加载点云 ---------------------------------
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);			//待滤波点云
	if (pcl::io::loadPCDFile("happy buddha.pcd", *cloud) < 0)
	{
		PCL_ERROR("\a点云文件不存在！\n");
		system("pause");
		return -1;
	}
	cout << "->加载点云的点数为：" << cloud->points.size() << endl;
	//============================================================================

	//----------------------------- 近似体素重心下采样 -----------------------------
	pcl::console::TicToc time;
	time.tic();
	cout << "->正在进行近似体素重心下采样..." << endl;
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_sub(new pcl::PointCloud<pcl::PointXYZ>);	//滤波后点云
	pcl::ApproximateVoxelGrid<pcl::PointXYZ> avg;	//创建滤波器对象
	avg.setInputCloud(cloud);						//设置待滤波点云
	avg.setLeafSize(0.002, 0.002, 0.002);			//设置体素边长
	avg.setDownsampleAllData(false);				//如果只有XYZ字段，则设置为false，如果对所有字段，如intensity，都进行下采样，则设置为true
	avg.filter(*cloud_sub);							//执行下采样，保存结果于cloud_sub
	cout << "->近似体素下采样用时：" << time.toc() / 1000 << " s" << endl;
	//============================================================================

	//------------------------------- 保存滤波点云 --------------------------------
	cout << "->正在保存滤波点云..." << endl;
	if (!cloud_sub->empty())
	{
		pcl::io::savePCDFileBinary("ApproximateVoxelGrid.pcd", *cloud_sub);
		cout << "->下采样点云的点数为" << cloud_sub->points.size() << endl;
	}
	else
	{
		PCL_ERROR("\a下采样点云为空！\n");
		system("pause");
		return -1;
	}
	//============================================================================

	//------------------------- 下采样前后对比可视化（选） --------------------------
	pcl::visualization::PCLVisualizer::Ptr viewer(new pcl::visualization::PCLVisualizer("下采样前后对比"));
	///原始点云
	int v1(0);
	viewer->createViewPort(0.0, 0.0, 0.5, 1.0, v1); //设置第一个视口在X轴、Y轴的最小值、最大值，取值在0-1之间
	viewer->setBackgroundColor(0, 0, 0, v1); //设置背景颜色，0-1，默认黑色（0，0，0）
	viewer->addText("original_Pt", 10, 10, "v1_text", v1);
	viewer->addPointCloud<pcl::PointXYZ>(cloud, "original", v1);
	///半径滤波后点云
	int v2(0);
	viewer->createViewPort(0.5, 0.0, 1.0, 1.0, v2);
	viewer->setBackgroundColor(0.3, 0.3, 0.3, v2);
	viewer->addText("filtered_Pt", 10, 10, "v2_text", v2);
	viewer->addPointCloud<pcl::PointXYZ>(cloud_sub, "sub", v2);
	///设置相关属性
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 2, "original", v1);
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 1, 0, 0, "original", v1);
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 2, "sub", v2);
	viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 0, 1, 0, "sub", v2);

	while (!viewer->wasStopped())
	{
		viewer->spinOnce(100);
		boost::this_thread::sleep(boost::posix_time::microseconds(100000));
	}
	//============================================================================

	return 0;
}

均匀采样

均匀采样的原理类似于体素化网格采样方法，同样是将点云空间进行划分，不过是以半径 = r 的球体，在当前球体所有点中选择距离球体中心最近的点替代所有点，注意，此时点的位置是不发生移动的。球体半径选取越大则采样之后的点云越少，处理速度变快，但会对原先点云过度模糊，网格选取越小，则作用相反。

均匀采样的特点是采样点分布均匀，不会移动点云点，准确度较高，但时间复杂度提升。

其核心代码如下：

1
2
3
4
5
pcl::UniformSampling<pcl::PointXYZ> form;   // 创建均匀采样对象
form.setInputCloud(cloud);                  //设置输入点云
form.setRadiusSearch(0.02f);                //设置半径大小,单位:m
form.filter(*after_cloud);                  //执行滤波处理

几何采样

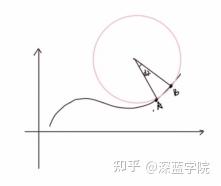
其原理是以点云的几何特征作为采样依据，这里以曲率为例。在点云中任意一点都存在某曲面，曲率计算示意图如图 2 所示，曲率越大，弧的弯曲程度越大，表示该地方的特征点越多，故在点云曲率越大的地方，采样点数越多，实现方法如下：

  1. 首先计算每个点的 K 领域，然后计算点到领域点的法线夹角值，以此来近似达到曲率的效果并提高计算效率，因为曲率越大的地方，夹角值越大。

  2. 设置一个角度阈值，当点的领域夹角值大于阈值时被认为是特征明显的区域，其余区域为不明显区域。

  3. 对明显和不明显区域进行均匀采样，采样数分别为 U*(1-V) 和 U*V,U 是目标采样数，V 是均匀采样性。

其特点是计算效率高，且局部点云的采样是均匀的，同时稳定性高，使得采样结果的抗噪性更强。

随机下采样

随机下采样的原理十分简单，如图 3 所示，首先指定下采样的点数，然后进行随机点去除进行采样操作, 得到图 3(b)。

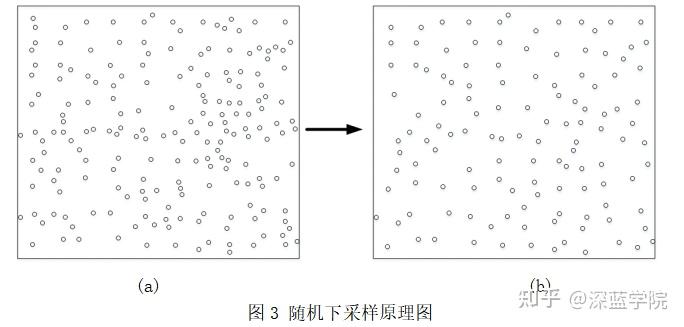
随机下采样的特点是能控制输出点云的数量，但随机性太大，可能剔除点云的关键数据。

其核心代码如下：

1
2
3
4
5
6
pcl::RandomSample<PointT> ran;     //创建滤波器对象
ran.setInputCloud(cloud);   //设置待滤波点云
ran.setSample(200);     //设置下采样点云的点数
ran.setSeed(1);      //设置随机函数种子点
ran.filter(*after_cloud);   //执行随机下采样滤波

上采样

增采样的原理如图 4 所示，当目前拥有的点云数据量较少时，如图 4(a)，通过内插点云的方法对目前的点云数据对进行扩充，如图 4(b)，达到保证基本形状不变的情况下增加点云。

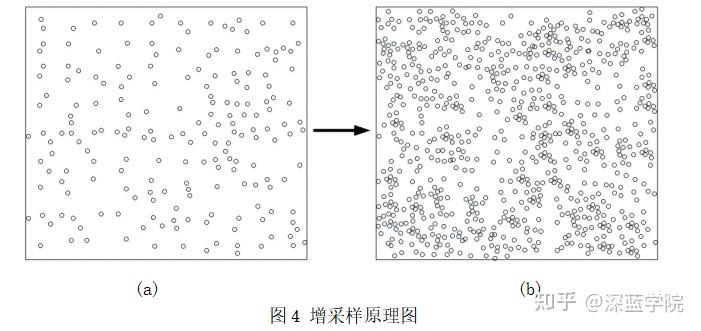
增采样的特点是可极大的增加点云数据，但由于内插点的不确定性会导致最后输出的结果不一定准确。

其核心代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
//创建增采样对象
pcl::MovingLeastSquares<pcl::PointXYZ,pcl::PointXYZ> filter;    
filter.setInputCloud(cloud);                     //设置输入点云
pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree;  //定义搜索方法
filter.setSearchMethod(kdtree);                  //设置搜索方法
filter.setSearchRadius(0.03);    //设置搜索邻域的半径为3cm  
//Upsampling 采样的方法还有 DISTINCT_CLOUD, RANDOM_UNIFORM_DENSITY
filter.setUpsamplingMethod(pcl::MovingLeastSquares<pcl::PointXYZ, pcl::PointXYZ>::SAMPLE_LOCAL_PLANE);     //对点云进行上采样
filter.setUpsamplingRadius(0.03);    //设置采样半径大小，3cm
filter.setUpsamplingStepSize(0.02);  //设置采样步长大小，2cm
filter.process(*after_cloud);      //执行采样操作

点云平滑

滑动最小二乘法采样

滑动最小二乘法采样的原理是将点云进行了滑动最小二乘法的映射，使得输出的点云更加平滑。

滑动最小二乘法的特点是适用于点云的光顺处理，但有时会牺牲表面拟合精度的代价来获得输出点云。

其核心代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
pcl::PointCloud<pcl::PointNormal>::Ptr smoothedCloud(new pcl::PointCloud<pcl::PointNormal>);   //定义法线
pcl::MovingLeastSquares<pcl::PointXYZ, pcl::PointNormal> filter;
pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree;  //定义搜索方法
filter.setInputCloud(cloud);    //设置输入点云
filter.setUpsamplingMethod();  //增加密度较小区域的密度对于holes的填补却无能为力，具体方法要结合参数使用
filter.setSearchRadius(10);// 用于拟合的K近邻半径。在这个半径里进行表面映射和曲面拟合。半径越小拟合后曲面的失真度越小，反之有可能出现过拟合的现象。
filter.setPolynomialFit(true);  //对于法线的估计是有多项式还是仅仅依靠切线。true为加多项式；false不加，速度较快
filter.setPolynomialFit(3);      // 拟合曲线的阶数
filter.setComputeNormals(true);  // 是否存储点云的法向量，true 为存储，false 不存储
filter.setSearchMethod(kdtree); //设置搜索方法
filter.process(*smoothedCloud); //处理点云并输出

总结：

总结一下，在下采样方法中，以体素化网格采样方法最为常用，因为其速度快，代码量少，且满足大多数时的点云处理要求；均匀采样虽然精度高，当耗时高，可以用于更追求精度的场合下；几何采样由于使用不多，方法很多，这里只是简答介绍了一下曲率采样，比较适用于不规则的且丰富表面特征的点云数据计算；随机下采样由于能准确控制点云的输出数量，但过于随机，较少使用；增采样用于增加点云数据，更适合用于解决曲面重建时点云数量缺少的问题；而滑动最小二乘法同样是对点云数量的扩充，但主要是对点云形状进行平滑处理，所以更适合用来对点云结构进行优化。

xiaohui3D Reconstruction

道虽迩，不行不至；事虽小，不为不成。